Raised cosine filter design.

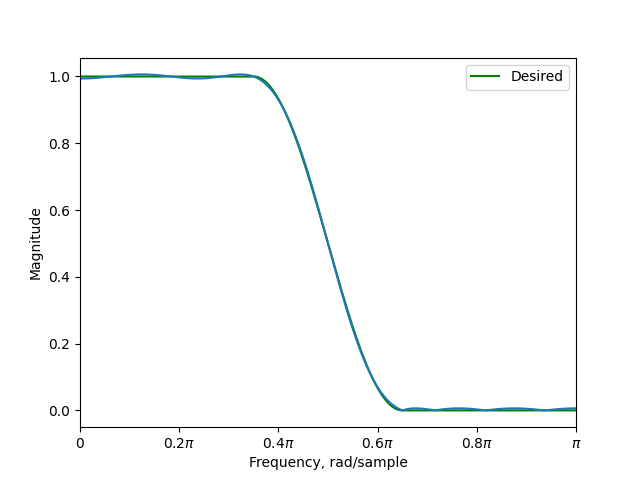
Design a raised cosine filter with a rolloff of 0.3.

import matplotlib.pyplot as plt
import numpy as np
from mplsignal import freqz_fir

from fird.designer import FIRDesigner
from fird.objective import RaisedCosineLinearObjective

o = RaisedCosineLinearObjective(0.3)
d = FIRDesigner(22, o)
d.solve()
h = d.get_impulse_response()
fig, ax = plt.subplots()
o.plot(ax, label="Desired")
freqz_fir(h, ax=ax, magnitude_scale="linear", style="magnitude")
ax.legend()
fig.show()

Display the impulse response. As expected every other coefficient is close to zero and the middle coefficient is close to 0.5.

print(h)
fig, ax = plt.subplots()
ax.stem(h)
fig.show()

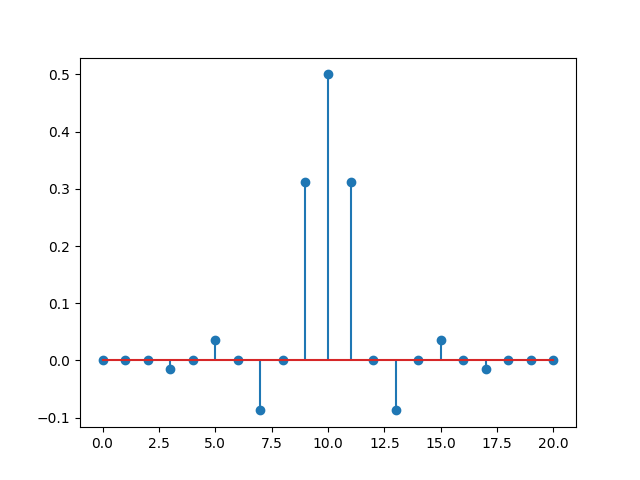
[-4.7770938e-08  1.1818022e-03  7.7605963e-09 -1.4592795e-02
  2.6864261e-08  3.6033765e-02 -3.1785043e-09 -8.7356219e-02
  2.4387249e-08  3.1164230e-01  4.9999998e-01  3.1164230e-01
  2.4387249e-08 -8.7356219e-02 -3.1785043e-09  3.6033765e-02
  2.6864261e-08 -1.4592795e-02  7.7605963e-09  1.1818022e-03
 -4.7770938e-08]

To make the coefficients exactly as expected, add a NyquistConstraint

from fird.constraint import NyquistConstraint  # noqa: E402

c = NyquistConstraint(2)
d = FIRDesigner(22, o, c)
d.solve()
h = d.get_impulse_response()
fig, ax = plt.subplots()
o.plot(ax, label="Desired")
freqz_fir(h, ax=ax, magnitude_scale="linear", style="magnitude")
ax.legend()
fig.show()

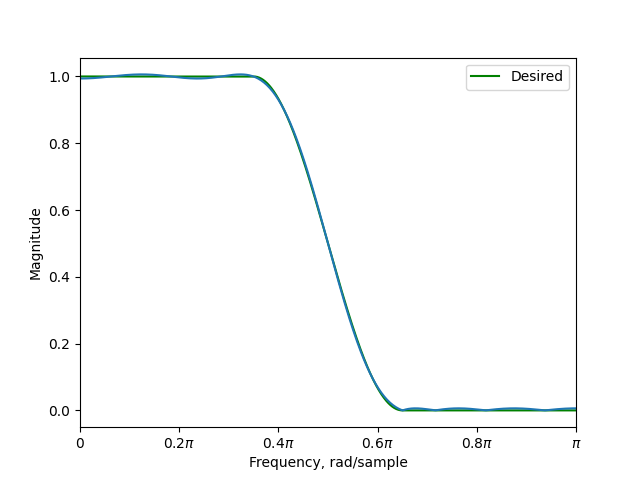
Now, the every other coefficient is exactly zero.

print(h)
fig, ax = plt.subplots()
ax.stem(h)
fig.show()

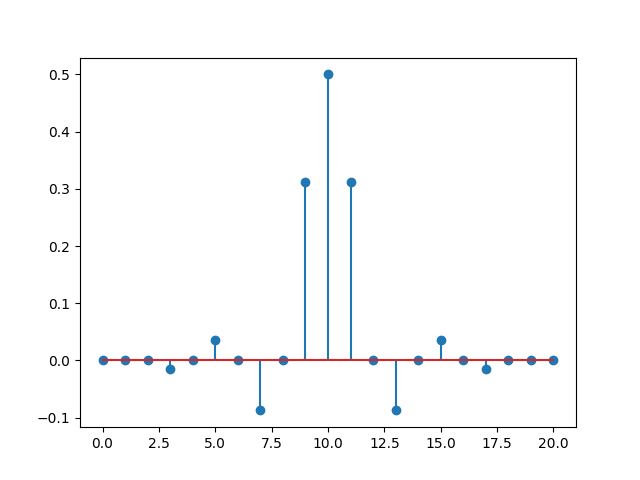
[ 0.          0.0011818   0.         -0.01459281  0.          0.03603375
  0.         -0.08735623  0.          0.3116423   0.5         0.3116423
  0.         -0.08735623  0.          0.03603375  0.         -0.01459281
  0.          0.0011818   0.        ]

It is also possible to design root raised cosine filters

from fird.objective import RootRaisedCosineLinearObjective  # noqa: E402

o = RootRaisedCosineLinearObjective(0.3)
d = FIRDesigner(12, o)
d.solve()
h = d.get_impulse_response()
fig, ax = plt.subplots()
o.plot(ax, label="Desired")
freqz_fir(h, ax=ax, magnitude_scale="linear", style="magnitude")
ax.legend()
fig.show()

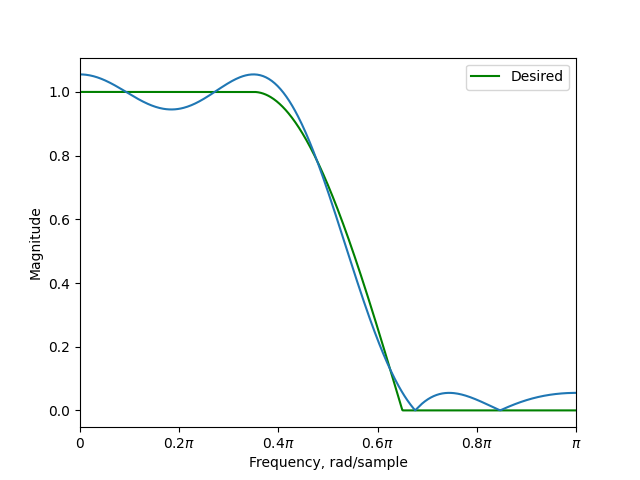
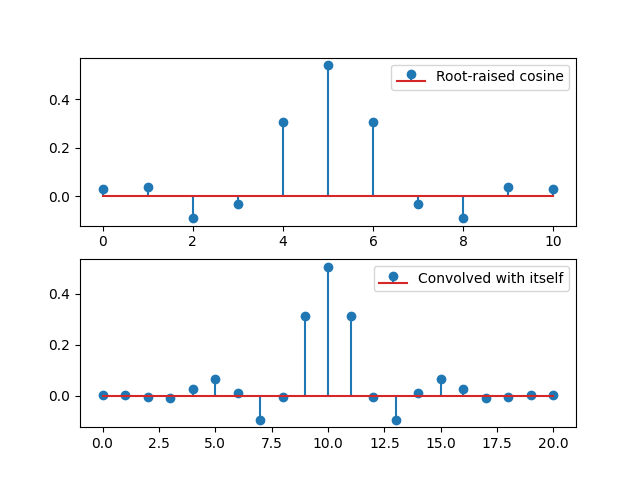
Here, the filter is not a Nyquist filter, but the convolution with itself should be.

fig, ax = plt.subplots(2, 1)
ax[0].stem(h, label="Root-raised cosine")
ax[0].legend()
ax[1].stem(np.convolve(h, h), label="Convolved with itself")
ax[1].legend()
fig.show()