Finite wordlength design.

It is almost always better to design filters taking the finite wordlength of the coefficients into account compared to rounding the coefficients after design.

import matplotlib.pyplot as plt
import numpy as np
from mplsignal import freqz_fir

from fird.designer import FIRDesigner
from fird.objective import PiecewiseLinearObjective

First, design a filter minimizing the approximation error using a filter order of 31 and continuous coefficients as reference.

o = PiecewiseLinearObjective([0, 0.3, 0.5, 1], [1, 1, 0, 0])
d = FIRDesigner(31, o)
d.solve()
h31 = d.get_impulse_response()

Redesign the filter using ten fractional bits for the coefficients.

fractional_bits = 10
d = FIRDesigner(31, o, fractional_bits=fractional_bits)
d.solve()
h31_q = d.get_impulse_response()

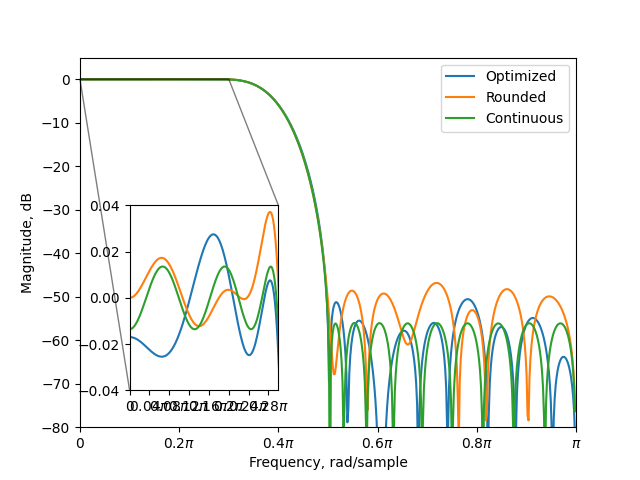
Plot the resulting filters, including the rounded version of the continuous design.

As seen, the optimized finite wordlength design is better than the rounded continuous design.

h31_rounded = np.round(h31 * 2**fractional_bits) / 2**fractional_bits

fig, ax = plt.subplots()
freqz_fir(h31_q, ax=ax, label="Optimized", style="magnitude")
freqz_fir(h31_rounded, ax=ax, label="Rounded", style="magnitude")
freqz_fir(h31, ax=ax, label="Continuous", style="magnitude")
ax.set_ylim(-80, 5)
ax.legend()
axins = ax.inset_axes([0.1, 0.1, 0.3, 0.5])
freqz_fir(h31_q, ax=axins, label="Optimized", style="magnitude")
freqz_fir(h31_rounded, ax=axins, label="Rounded", style="magnitude")
freqz_fir(h31, ax=axins, label="Continuous", style="magnitude")
axins.set_xlim(0, 0.3 * np.pi)
axins.set_ylim(-0.04, 0.04)
axins.xaxis.label.set_visible(False)
axins.yaxis.label.set_visible(False)
ax.indicate_inset_zoom(axins, edgecolor="black")
fig.show()

It is also possible to obtain the coefficients as an APyTypes fixed-point array.

d.get_impulse_response(apytypes=True)

APyFixedArray(
    [   1, 2047, 2045,    0,    7,    7, 2040, 2029, 2047,   32,   27, 2013, 1968, 2047,
      202,  383,  383,  202, 2047, 1968, 2013,   27,   32, 2047, 2029, 2040,    7,    7,
        0, 2045, 2047,    1],
    int_bits=1,
    frac_bits=10
)