Sparse filter design.

Sparse filters can be easily designed. You just need to decide if you want to minimize the approximation error subject to complexity of minimize the complexity subject to the approximation error.

import matplotlib.pyplot as plt
import numpy as np
from mplsignal import freqz_fir

from fird.constraint import MaxNonzeroCoefficientsConstraint, PiecewiseLinearConstraint
from fird.designer import FIRDesigner
from fird.objective import (
    L1CoefficientsObjective,
    MaxNonzeroCoefficientsObjective,
    PiecewiseLinearObjective,
)

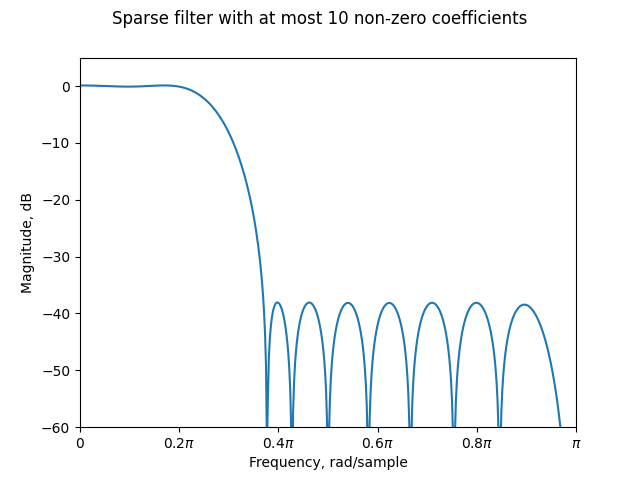
Let us start by designing a lowpass filter of order 31, but with at most ten of the sixteen variables/coefficients being zero (20 of the 32 taps due to symmetry).

o = PiecewiseLinearObjective([0, 0.2, 0.37, 1], [1, 1, 0, 0])
c = MaxNonzeroCoefficientsConstraint(10)
d = FIRDesigner(31, o, c)
d.solve()
h31_10 = d.get_impulse_response()
fig, ax = plt.subplots()
freqz_fir(h31_10, ax=ax, style="magnitude")
ax.set_ylim(-60, 5)
fig.suptitle("Sparse filter with at most 10 non-zero coefficients")
fig.show()

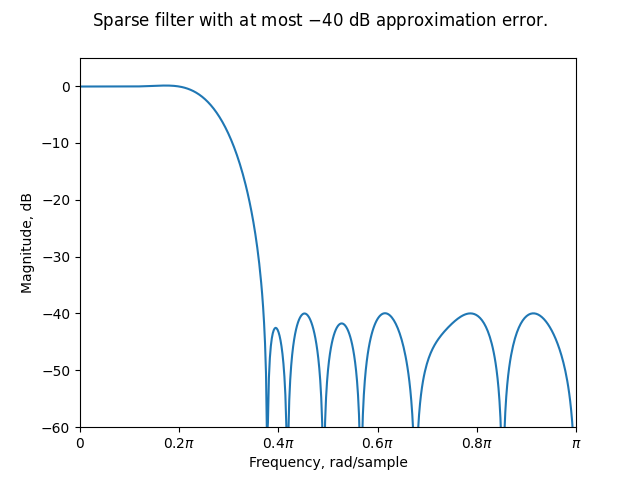
The alternative is to design a filter of order 31 minimizing the number of non-zero coefficients subject to a given approximation error.

c = PiecewiseLinearConstraint([0, 0.2, 0.37, 1], [1, 1, 0, 0], [0.01, 0.01])
o = MaxNonzeroCoefficientsObjective()

d = FIRDesigner(31, o, c)
d.solve()
h31_sparse = d.get_impulse_response()
fig, ax = plt.subplots()
freqz_fir(h31_sparse, ax=ax, style="magnitude")
ax.set_ylim(-60, 5)
fig.suptitle("Sparse filter with at most $-40$ dB approximation error.")
fig.show()

The impulse responses of the designed filters can be examined to see the sparsity.

print("Non-zero filter taps in h31_10:", np.count_nonzero(h31_10))
print("Non-zero filter taps in h31_sparse:", np.count_nonzero(h31_sparse))

fig, ax = plt.subplots(2, 1, layout="constrained")
ax[0].stem(h31_10)
ax[0].set_title("Impulse response of h31_10")
ax[1].stem(h31_sparse)
ax[1].set_title("Impulse response of h31_sparse")
fig.show()

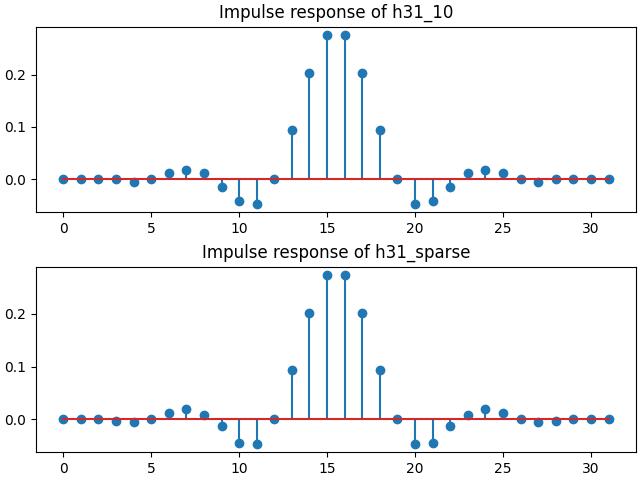
Non-zero filter taps in h31_10: 20
Non-zero filter taps in h31_sparse: 22

It is also possible to convert between constraints and objectives. For instance, the previous design can be done by converting the constraint to an objective.

cconv = o.to_constraint(10)
oconv = c.to_objective()
d = FIRDesigner(31, oconv, cconv)
d.solve()
h31_10_conv = d.get_impulse_response()

The results asshould be the the same.

np.testing.assert_allclose(h31_10, h31_10_conv)

Finally, it is also possible to approximate a sparse design by minimizing the L1-norm of the coefficients. This will avoid the potentially costly integer programming.

o = L1CoefficientsObjective()
d = FIRDesigner(31, o, c)
d.solve()
h31_l1 = d.get_impulse_response()
fig, ax = plt.subplots(2, 1, layout="constrained")
freqz_fir(h31_l1, ax=ax[0], style="magnitude")
ax[0].set_ylim(-60, 5)
ax[1].stem(h31_l1)
fig.suptitle("L1-norm minimized filter with at most $-40$ dB approximation error.")
fig.show()
print("Non-zero filter taps in h31_l1:", np.count_nonzero(h31_l1))

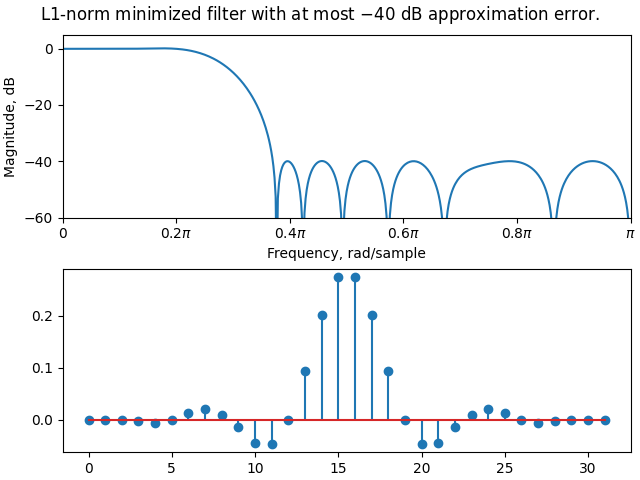
Non-zero filter taps in h31_l1: 28